El problema del senderista

Lo cierto es que tenía apuntado este problema en un papel, guardado en la estantería de mi cuarto, desde hacía unos cuantos meses. Y, como físico en potencia (que no en acto), aún no sé muy bien si está bien expresado, o si se le puede sacar más jugo, pero allá va.

Resulta que a mi familia (sobre todo a mis padres), les gusta el senderismo. Les atrae viajar a la naturaleza, incluso perderse un poco por aquella. También hay cuestas grandes, pero bueno, se suben más despacio. Las bajadas son lo que a mí me mosquean. Bajadas empinadas, en las que no puedes dejarte caer por el peso de la mochila, la sujección de las botas y la puesta en riesgo de la propia integridad física. Normalmente, se bajan con los pies ladeados, dejado el exterior del tobillo hacia la parte que queremos bajar. ¿Mi solución? Bajar haciendo eses.

Cuando un senderista baja por una colina, al cabo de recorrer una distancia "s", ha descendido una altura "h", estando estos dos parámetros relacionados por el ángulo de la pendiente, alfa. Hasta ahí bien, ¿no? Como la diferencia de altura es una diferencia de potencial, el trabajo que realizamos al subir o bajar una altura h, y vendrá dado por

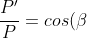Siendo m la masa del senderista (mochila incluida) y g la aceleración de la gravedad de la Tierra, que suponemos constante en esa altura h. Estamos obviando el rozamiento del cuerpo con el aire, las botas con el suelo y de los músculos y huesos entre sí.

Si la diferencia de energía es la misma, ¿Por qué bajo haciendo eses? Porque aunque el trabajo potencial sea el mismo, la potencia que tengo que desarrollar es menor. La potencia se define como la derivada del trabajo con respecto del tiempo. Si derivamos:

Llamaremos a la componente de la velocidad paralela a s velocidad de bajada, 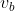. Cuando no bajamos paralelos a s, la velocidad a la que bajamos v, es composición de la velocidad de bajada, 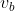, por la cual realizamos una potencia P, y una velocidad normal a s, 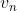, que no influye en el trabajo potencial porque es perpendicular a s.

Siendo beta el ángulo que hay entre la cuesta y la velocidad que nosotros llevamos. Entonces, la potencia que nosotros tenemos que desarrollar en las piernas para ir frenando, será:

Y la proporción entre las dos potencias es de

Lo que quiere decir que, cuanto mayor sea beta, menor potencia tendré que desarrollar con respecto a la potencia de bajada, P. En resumidas cuentas, podríamos decir que cuantas más me desvíe en la bajada (mayor ángulo con respecto a la pendiente), menos me cuesta ir frenando la caída (o subiendo la cuesta). Claro, que como se recorre mayor distancia, aumentará el rozamiento y habrá un término medio entre hacer eses y bajar directamente.